Samuel Cormier-Iijima’s home on the web

Alternative Combinatorial Gray Codes

A PDF version of this article can be downloaded here.

Gray codes have numerous applications in a variety of fields, including error correction, encryption, databases, and puzzles. The standard Gray code is the Binary Reflected Gray Code (BRGC), but there are many other possible minimal change orderings on binary tuples as well as other combinatorial objects. These include long-run (maximal run-lengths), balanced, monotonic, and single-track Gray codes. This article gives an overview of each of these types of codes along with the motivation behind using them.

Introduction

An $n$-digit $R$-ary Gray code (sequence) of period $m$ is a sequence $G = (g_k)_{k=0}^{m-1}$ of $m$-many distinct $n$-digit vectors (or strings) consisting of digits taken from the set $\mathbb{Z}_R = \mathbb{Z}/R\mathbb{Z} = \{0, 1, \cdots, R-1\}$, such that any two consecutive vectors differ in only one digit by at most 1. If $g_0$ and $g_{m-1}$ also share this property, then the code is said to by cyclic (or a Gray cycle); if the code contains all $R^n$ possible vectors, that is, if $m = R^n$, then it is said to be complete.

A binary Gray code can be seen another way: by associating the $n$-bit binary vectors with nodes in the hypercube graph $Q_n$, a Gray code $G$ defines a Hamiltonian path on the subgraph of $Q_n$ induced by the vectors in $G$. If the code is cyclic, then this path is in fact a Hamiltonian cycle, and if the code is complete, then the path visits all nodes in $Q_n$.

A third way to describe a Gray code is by the sequence of positions that change between consecutive strings. If $G$ is an $n$-digit cyclic binary Gray code, then there are integers $\delta_0, \delta_1, \cdots, \delta_{m-1}$, called the transition (delta) sequence of $G$, such that \[ g_{k+1} = 2^{\delta_k} \oplus g_k \, , \text{ for } k \in \mathbb{Z}_m \] where the vectors $g_k$ are interpreted as binary numbers. Note that the elements of the transition sequence correspond to edges in the Hamiltonian path described by the Gray code.

The most well-known binary Gray code, the binary reflected Gray code (BRGC), was developed and patented by Frank Gray in 1953 for use in converting analog signals to digital ones. The BRGC $\Gamma_n = (\gamma_n(0), \cdots, \gamma_n(n-1))$ can be defined recursively by letting $\Gamma_0$ be the empty string and writing \[ \Gamma_{n+1} = (0\gamma_n(0), \cdots, 0\gamma_n(n-1), 1\gamma_n(n-1), \cdots, 1\gamma_n(0)) \] In general, however, there are many different ways to define Gray codes, and some of these alternative definitions have certain desirable properties. The rest of this paper will review the other Gray codes that have been studied in the literature. The survey of combinatorial Gray codes in [8] provides a more in-depth review of Gray codes, especially as applied to other combinatorial objects such as permutations, trees, and partitions.

Alternative Gray Codes

Single-Track Gray Codes

Gray codes can be used in analog-to-digital rotary encoders, where the absolute angular position of a rotating wheel is measured by encoding the values read off of $n$ concentrically-arranged tracks. Here, if a regular binary encoding were used, a small difference in the angle of the wheel could result in a large difference in the binary representation of the angle, leading to a large measurement error. (This is especially true if mechanical contacts are used, leading to the need for switch debouncing). If instead a Gray code of period $m$ is used, the error in angular position due to this uncertainty in measurement can be bounded to within $2\pi/m$.

If high accuracy is required, the large number of tracks that are needed can lead to problems, especially when designing small-scale devices. This problem can be solved using single-track Gray codes (proposed in [5]) where instead multiple reading heads are used on a single track. For this to be possible with a Gray code $G = (g_1, g_2, \cdots, g_m)$, the component tracks (sequences) \[ C_j(G) = (g_1^j, g_2^j, \cdots, g_m^j) \] for $j \in \mathbb{Z}_n$ must be cyclic shifts of each other. That is, if $E$ is the left-shift operator on $n$-digit strings, then for every $j \in \mathbb{Z}_n$, \[ C_j(G) = E^{t_j}(C_0(G)) \] and the $t_j$ are called the head positions of the Gray code.

A construction due to [5] gives single-track Gray codes of length $nt$ for every $n \geq 4$ and \[ 2 \leq t \leq 2^{n-1-\left \lceil \sqrt{2(n-3)} \right \rceil} \] While this allows generating codes of many different lengths, it is far from the optimal length of $2^n$ for an $n$-digit code. The authors of [2] show that single-track $n$-digit codes of period $2^n - 2n$ can be constructed whenever $n$ is a power of two. In general, however, the construction takes “seed codes” of period $n$ and produces single-track codes having periods that are multiples of $n$; such seed codes have been found for small $n$ in [14].

Balanced Gray Codes

Although the binary reflected Gray code is useful in many scenarios, it is not optimal in certain cases because of a lack of “uniformity” [1]. In balanced Gray codes, we seek to make the number of changes in each coordinate position as close as possible. To make this more precise, let $G$ be a $R$-ary complete Gray cycle having transition sequence $(\delta_k)$; the transition counts (spectrum) of $G$ are the collection of integers defined by \[ \lambda_k = |\{ j \in \mathbb{Z}_{R^n} : \delta_j = k \}| \, , \text { for } k \in \mathbb{Z}_R \] We say that a Gray code is uniform or uniformly balanced if its transition counts are all equal, in which case we have $\lambda_k = R^n / n$ for all $k$. Clearly, when $R = 2$, such codes exist only if $n$ is a power of 2. A construction for this case can be found in [13]. Otherwise, if $n$ does not divide $R^n$ evenly, the best we can do is to construct well-balanced codes where every transition count is either $\lfloor R^n / n \rfloor$ or $\lceil R^n / n \rceil$. Gray codes can also be exponentially balanced if all of their transition counts are adjacent powers of two. The existence of such Gray codes was established in [12].

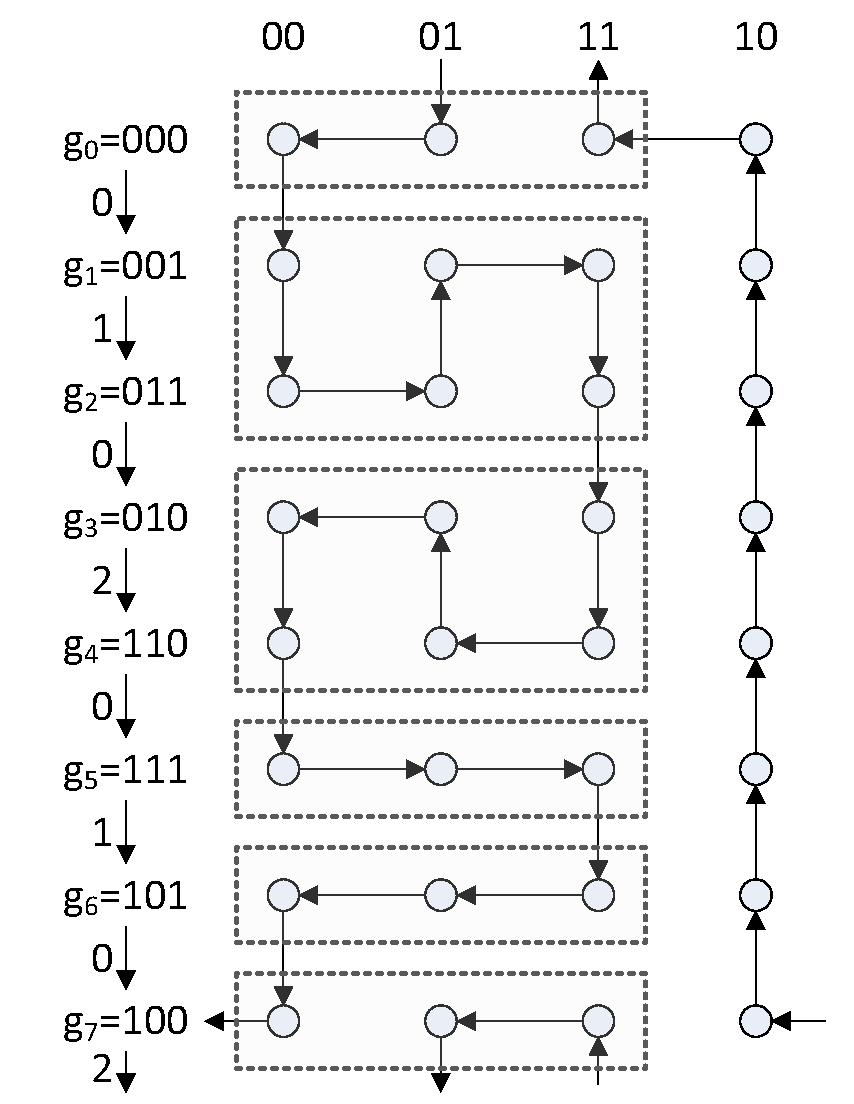
We will now show a construction for well-balanced binary Gray codes (following that of [3] and [6]) which allows us to generate a $n$-digit balanced Gray code for every $n$. The main principle is to inductively construct a $(n+2)$-digit Gray code $G'$ given an $n$-digit Gray code $G$ in such a way that the balanced property is preserved. To do this, we consider partitions of $G = g_0, \cdots, g_{2^n-1}$ into an even number $L$ of non-empty blocks of the form \[ \{g_0\}, \{g_1, \cdots, g_{k_2}\}, \{g_{k_2+1}, \cdots, g_{k_3}\}, \cdots, \{g_{k_{L-2}+1}, \cdots, g_{-2}\}, \{g_{-1}\} \] where $k_1 = 0$, $k_{L-1} = -2$, and $k_{L} = -1$ (mod $2^n$). This partition induces a $(n+2)$-digit Gray code in given by \[ \begin{aligned} & 00g_0, \\ & 00g_1, \cdots, 00g_{k_2}, 01g_{k_2}, \cdots, 01g_1, 11g_1, \cdots, 11g_{k_2}, \\ & 11g_{k_2+1}, \cdots, 11g_{k_3}, 01g_{k_3}, \cdots, 01g_{k_2+1}, 00g_{k_2+1}, \cdots, 00g_{k_3}, \cdots, \\ & 00g_{-2}, 00g_{-1}, 10g_{-1}, 10g_{-2}, \cdots, 10g_0, 11g_0, 11g_{-1}, 01g_{-1}, 01g_0 \end{aligned} \] This process can be more easily visualized in Figure 2, where the 3-digit Gray code defined by the transition sequence 01020102 is extended to a 5-digit code using the partition $\{g_0\}, \{g_1, g_2\}, \{g_3, g_4\}, \{g_5\}, \{g_6\}, \{g_7\}$. The reason for the “notch” in the first and last rows is so that the transition between $g_0$ and $g_{-1}$ is included in the new Gray code.

If we define the transition multiplicities $m_i = |\{ j : \delta_{k_j} = i, 1 \leq j \leq L \}|$ to be the number of times the digit in position $i$ changes between consecutive blocks in a partition, then for the $(n+2)$-digit Gray code induced by this partition the transition spectrum $\lambda'_k$ is \[ \lambda'_k = \begin{cases} 4 \lambda_k - 2 m_k, \, \text{ if } 0 \leq k < n \\ L, \, \text{ otherwise } \end{cases} \] This can be seen by looking at the diagram; the transition between $g_i$ and $g_{i+1}$ occurs exactly four times if $g_i$ and $g_{i+1}$ are in the same partition, and exactly twice otherwise (the “notch” also ensures that this happens for $g_{-1}$ and $g_0$). Also, every partition contains exactly one transition for each of the digits $n$ and $n+1$.

The delicate part of this construction is to find an adequate partitioning of a balanced $n$-digit Gray code such that the code induced by it remains balanced. The details, as well as an extension of this construction to the $R$-ary case, can be found in [3], who show that uniform codes can be found when $R \equiv 0 \mod 4$ and $R^n \equiv 0 \mod n$.

Long-Run Gray Codes

Another way of balancing Gray codes is to maximize the distance between consecutive changes of digits in the same position. That is, we would like to find a $n$-digit Gray code $G$ with transition sequence $(\delta_k)$ such that the minimum run length of $G$ \[ \text{mrl}(G) = \min \{ |i-j| : \delta_i = \delta_j, i \neq j \} \] is maximal over all $n$-digit Gray codes. As an example, the minimum run length for every binary reflected Gray code is $\text{mrl}(BRGC) = 2$, since the bit in position 0 changes at every two steps. A 5-digit Gray code which has a minimum run length of 4 is shown in Figure 3.

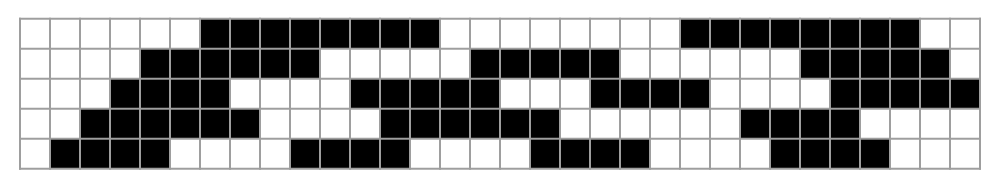
Let $\text{mrl}(n)$ be the maximum possible value of $\text{mrl}(G)$ over all $n$-bit Gray codes $G$. The first few values of $\text{mrl}(n)$ are known for $n < 8$, and can easily be found using an exhaustive backtracking search. They are \[ \text{mrl}(n) = 1, 2, 2, 2, 4, 4, 5 \text{ for } n = 1, 2, \cdots, 7 \] This sequence has been characterized by [4], who show that, for integers $a$ and $b$ satisfying $(a-1)(2^a - 2a - 6) \leq 2^b$, $\text{mrl}(a+b) \geq 2 \min \{ a-1, \text{mrl}(b) \}$. This recurrence relation, when solved, yields the lower bound \[ \text{mrl}(n) \geq n - \lfloor 2.001 \lg n \rfloor \text{ for } n \geq 2 \] The proof involves decomposing the hypercube $Q_n$ into $Q_a \times Q_b$ and merging a “stream” in $Q_a$ (a set of $2^a$ walks induced by a sequence of step permutation on $Q_a$ taking vertices to their neighbors) and a Hamiltonian path in $Q_b$, but the details are slightly tricky and so are omitted here.

Monotonic Gray Codes

The last type of Gray code that we will examine is called monotonic. These codes are useful in the theory of interconnection networks, especially for minimizing dilation for linear arrays of processors [10]. If we define the weight of a binary string to be the number of 1`s in the string, then although we clearly cannot have a Gray code with strictly increasing weight, we may want to approximate this by having the code run through two adjacent weights before reaching the next one.

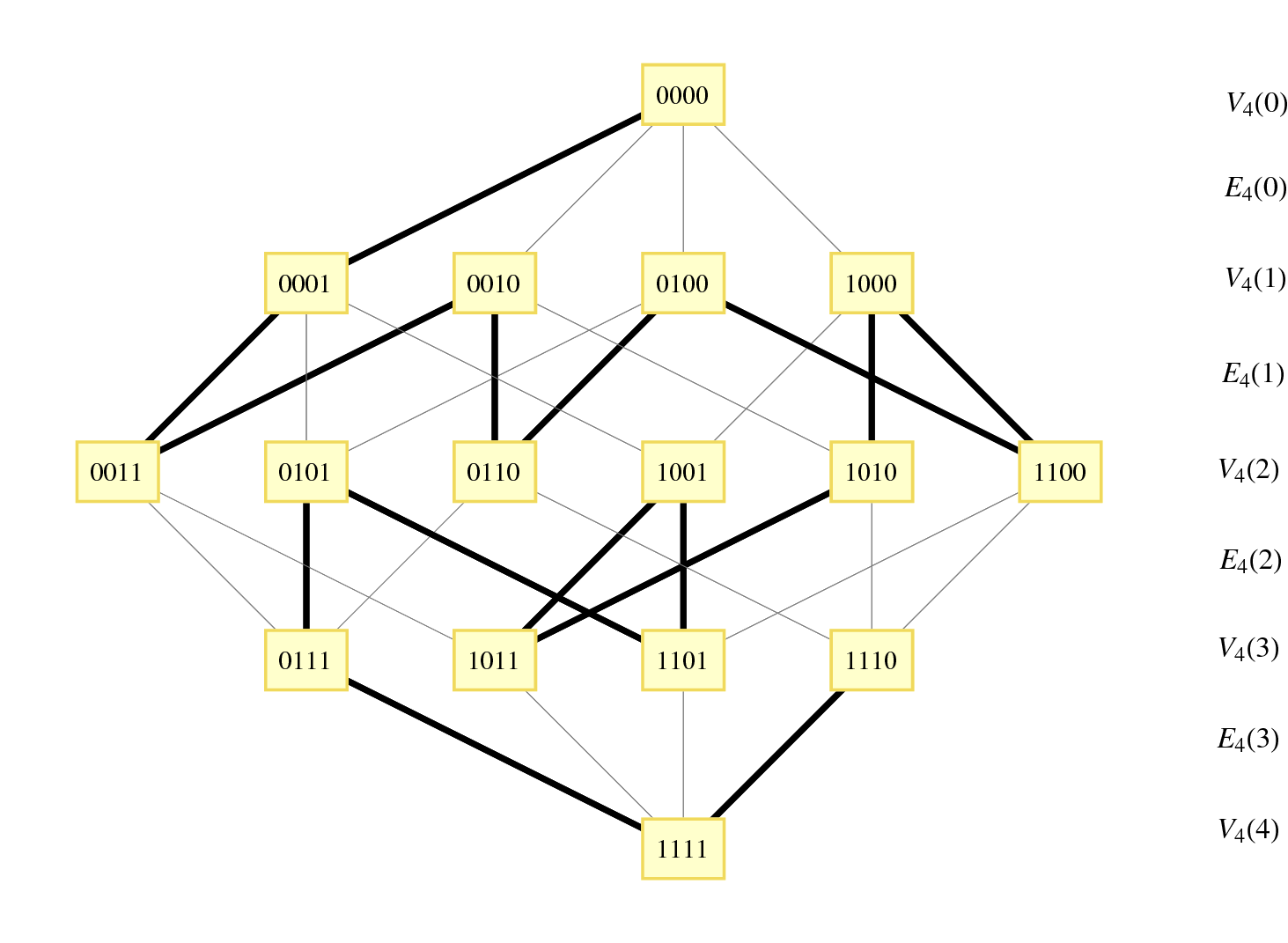
We can formalize the concept of monotone Gray codes as follows: consider the partition of the hypercube $Q_n = (V_n, E_n)$ into levels of vertices that have equal weight, i.e. \[ V_n(i) = \{ v \in V_n : v \text{ has weight } i \} \] for $0 \leq i \leq n$. These levels satisfy $|V_n(i)| = \binom{n}{i}$. Let $Q_n(i)$ be the subgraph of $Q_n$ induced by $V_n(i) \cup V_n(i+1)$, and let $E_n(i)$ be the edges in $Q_n(i)$. A monotonic Gray code is then a Hamiltonian path in $Q_n$ such that whenever $\delta_1 \in E_n(i)$ comes before $\delta_2 \in E_n(j)$ in the path, then $i \leq j$. Such a code when $n = 4$ is shown in Figure 4.

An elegant construction of monotonic $n$-digit Gray codes for any $n$ was found in [10]. The idea is to recursively build subpaths $P_{n,j}$ of length $2 \binom{n}{j}$ having edges in $E_n(j)$. We define $P_{1,0} = (0, 1)$, $P_{n,j} = \emptyset$ whenever $j < 0$ or $j \geq n$, and \[ P_{n+1,j} = 1P^{\pi_n}_{n,j-1}, 0P_{n,j} \] otherwise. Here, $\pi_n$ is a suitably-defined permutation and $P^{\pi}$ refers to the path $P$ with its coordinates permuted by $\pi$. These paths give rise to two monotonic $n$-digit Gray codes $G_n^{(1)}$ and $G_n^{(2)}$ given by \[ G_n^{(1)} = P_{n,0} P_{n,1}^R P_{n,2} P_{n,3}^R \cdots \text{ and } G_n^{(2)} = P_{n,0}^R P_{n,1} P_{n,2}^R P_{n,3} \cdots \] The choice of $\pi_n$ which ensures that these codes are indeed Gray codes turns out to be $\pi_n = E^{-1}(\pi_{n-1}^2)$. The first few values of $P_{n,j}$ are shown in Table 1.

$P_{n,j}$	$j=0$	$j=1$	$j=2$	$j=3$
$n=1$	0, 1
$n=2$	00, 01	10, 11
$n=3$	000, 001	100, 110, 010, 011	101, 111
$n=4$	0000, 0001	1000, 1100, 0100, 0110, 0010, 0011	1010, 1011, 1001, 1101, 0101, 0111	1110, 1111

These monotonic Gray codes can be efficiently implemented in such a way that each subsequent element can be generated in $O(n)$ time. The algorithm is most easily described using coroutines, and an example in Python can be found in Appendix A. Examples of the Gray codes generated by this algorithm when $n = 5, 6$ are shown in Figure 5 and Figure 6.

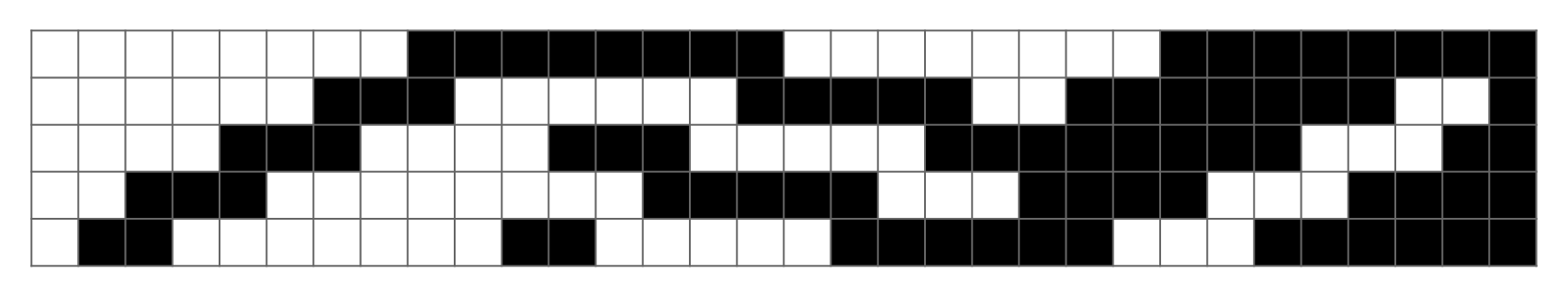
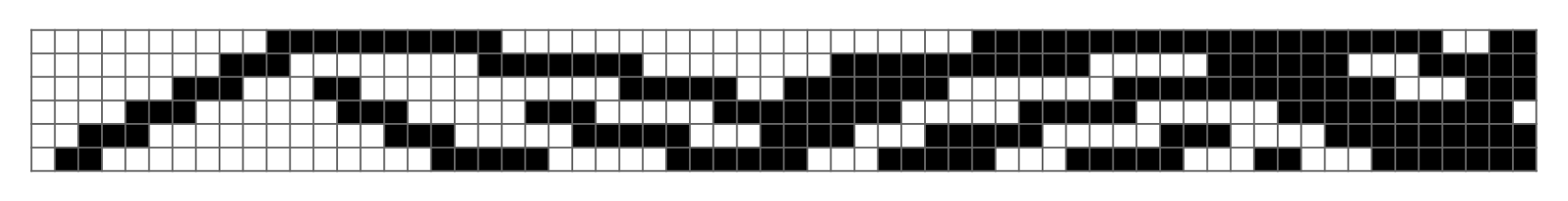
Monotonic codes have an interesting connection to the Lovász conjecture, which states that every connected vertex-transitive graph contains a Hamiltonian path. The “middle-level” subgraph $Q_{2n+1}(n)$ is vertex-transitive (that is, its automorphism group is transitive, so that each vertex has the same “local environment” and cannot be differentiated from the others, since we can relabel the coordinates as well as the binary digits to obtain an automorphism) and the problem of finding a Hamiltonian path in this subgraph is called the “middle-levels problem”, which can provide insights into the more general conjecture. The question has been answered affirmatively for $n \leq 15$, and the construction in [9] ensures a Hamiltonian path of length at least $0.839N$ where $N$ is the number of vertices in the middle-level subgraph. Both the Lovász conjecture and the middle-levels problem remain open.

Conclusion

There are many additional types of Gray codes which we have not discussed. These include circuit codes, which are closely related to long-run Gray codes, but introduce the additional requirement that for some given $d \leq \text{mrl}(G)$, $\delta(g_i, g_j) \geq d$ whenever $\|i-j\| \geq d$. When $d = m = 2$, these are also called snake-in-a-box or coil-in-a-box codes [7]. These types of codes have error-correcting properties that make them useful in information theory. Also, $R$-ary Gray codes for $R > 2$ have interesting applications to other areas of combinatorics, such as enumerating trees in a minimal change ordering. A much broader look at the topic can be found in [8], which is highly-recommended reading for anyone interested in the subject.

Appendix A: Monotonic Gray Codes in Python

Note that the function pi(n) can be memoized for increased performance.

def rotate_right(x, n):
    return x[-n:] + x[:-n]

def pi(n):
    if n <= 1:
        return (0,)
    x = pi(n - 1) + (n - 1,)
    return rotate_right(tuple(x[k] for k in x), 1)

def p(n, j, reverse=False):
    if n == 1 and j == 0:
        if not reverse:
            yield (0,)
            yield (1,)
        else:
            yield (1,)
            yield (0,)
    elif j >= 0 and j < n:
        perm = pi(n - 1)
        if not reverse:
            for x in p(n - 1, j - 1):
                yield (1,) + tuple(x[k] for k in perm)
            for x in p(n - 1, j):
                yield (0,) + x
        else:
            for x in p(n - 1, j, reverse=True):
                yield (0,) + x
            for x in p(n - 1, j - 1, reverse=True):
                yield (1,) + tuple(x[k] for k in perm)

def monotonic(n):
    for i in range(n):
        for x in (p(n, i) if i % 2 == 0 else p(n, i, reverse=True)):
            yield x

References

1. G. S. Bhat and C. D. Savage, “Balanced Gray codes,” Electronic Journal of Combinatorics, vol. 3, no. 1, p. R25, 1996.
2. T. Etzion and K. G. Paterson, “Near optimal single-track Gray codes,” Information Theory, IEEE Transactions on, vol. 42, no. 3, p. 779–789, 2002.
3. M. Flahive and B. Bose, “Balancing cyclic R-ary Gray codes,” the electronic journal of combinatorics, vol. 14, no. 31, p. 1, 2007.
4. L. Goddyn and P. Gvozdjak, “Binary gray codes with long bit runs,” the electronic journal of combinatorics, vol. 10, no. 27, p. 1, 2003.
5. A. P. Hiltgen, K. G. Paterson, and M. Brandestini, “Single-track Gray codes,” IEEE Transactions on Information Theory, vol. 42, no. 5, p. 1555–1561, 1996.
6. D. E. Knuth, The art of computer programming. Volume 4, fascicle 2. Generating all tuples and permutations. Addison-Wesley, 2005.
7. K. G. Paterson and J. Tuliani, “Some new circuit codes,” Information Theory, IEEE Transactions on, vol. 44, no. 3, p. 1305–1309, 2002.
8. C. Savage, “A survey of combinatorial Gray codes,” SIAM review, vol. 39, no. 4, p. 605–629, 1997.
9. C. D. Savage, “Long cycles in the middle two levels of the Boolean lattice,” in Ars Combin, 1997.
10. C. D. Savage and P. Winkler, “Monotone Gray codes and the middle levels problem,” Journal of Combinatorial Theory, Series A, vol. 70, no. 2, p. 230–248, 1995.
11. M. Schwartz and T. Etzion, “The structure of single-track Gray codes,” Information Theory, IEEE Transactions on, vol. 45, no. 7, p. 2383–2396, 2002.
12. I. N. Suparta, “A simple proof for the existence of exponentially balanced Gray codes,” Electron. J. Combin, vol. 12, 2005.
13. D. G. Wagner and J. West, “Construction of uniform Gray codes,” in Proceedings of the Twentieth Manitoba Conference on Numerical Mathematics and Computing: September 27-29, 1990, Winnipeg, Canada, 1991, p. 217.
14. I. Zinovik, D. Kroening, and Y. Chebiryak, “Computing binary combinatorial gray codes via exhaustive search with SAT solvers,” Information Theory, IEEE Transactions on, vol. 54, no. 4, p. 1819–1823, 2008.